Kernel Sequential Monte Carlo

February 15, 2016Importance Sampling, Inference, Monte Carlo, SMCIngmar

Heiko Strathmann, Brooks Paige, Dino Sejdinovic and I updated our draft on Kernel Sequential Monte Carlo (on the arxiv). Apart from locally adaptive covariance matrices for Gaussian proposals in various SMC algorithms, we also look at gradient emulators – both for targets that do not admit a first (gradient emulators) or even second derivative (locally adaptive covariance).
The emulators can be used in different ways, either as proposals for a MCMC rejuvenation step in SMC or as importance densities directly – for example in Population Monte Carlo.
We found especially the gradient emulator to be rather sensitive to the variance of the fit. Not Rao-Blackwellizing across importance densities used in a PMC iteration leads to gigantic estimated gradients and an exploding algorithm, while using a weighted streaming fit of the emulator with Rao-Blackwellization works just fine.
Plus we evaluate on the Stochastic volatility target from Nicolas SMC^2 paper, which is a much more nicer benchmark that what we had in the last draft (the plot being the targets marginals). Any feedback please send my way.

On the Geometric Ergodicity of Hamiltonian Monte Carlo

February 10, 2016Inference, mcmc, Monte Carlo, Numerics, statsIngmar

This remarkable arXival by Sam Livingstone, Betancourt, Byrne and Girolami takes a look at the conditions under which Hybrid/Hamiltonian Monte Carlo is ergodic wrt a certain distribution $\pi$ , and, in a second step, under which it will converge in total variation at a geometric rate. A nice feature being that they even prove that setting the integration time dynamically can lead to the sampler yielding geometric rate for a larger class of targets. Under idealized conditions for the dynamic integration time and, admittedly, in a certain exponential family.

Whats great about this paper, apart from the results, is how it manages to give the arguments in a rather accessible manner. Considering the depth of the results that is. The ideas are that

the gradient should at most grow linearly
for the gradient of $\pi$ to be of any help, it cannot lead further into the tails of the distribution or vanish (both assumption 4.4.1)
as we approach infinity, every proposed point thats closer to the origin will be accepted (assumption 4.4.2)

If the gradient grows faster than linear, numerics will punch you in the face. That happened to Heiko Strathmann and me just 5 days ago in a GradientIS-type algorithm, where an estimated gradient had length $10^{144}$ and led to Nirvana. If not the estimation is the problem but the actual gradient, of course you have the same effect. The second assumption is also very intuitive: if the gradient leads into the tails, then it hurts rather than helps convergence. And your posterior is improper. The final assumption basically requires that your chance to improve by proposing a point closer to the origin goes to $1$ the further you move away from it.

A helpful guidance they provide is the following. For a class of exponential family distributions given by 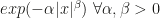$exp(-\alpha|x|^\beta)~\forall \alpha,\beta >0$ , whenever the tails of the distribution are no heavier than Laplace ( $\beta \geq 1$ ) and no thinner than Gaussian ( $\beta \leq 2$ ), HMC will be geometrically ergodic. In all other cases, it won’t.

Another thing that caught my eye was their closed form expression for the proposal after 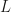$L$ leapfrog steps with stepsize $\epsilon$ , eq. (13):

Capture d’écran 2016-02-09 à 21.28.00

Which gives me hope that one should be able to compute the proposal probability after any number of leapfrog steps as long as $\nabla \log \pi$ is invertible and thus a Jacobian exists to account for the transformation of $p_0$ hidden in the $x_{i\epsilon}$ . A quick check with $\pi$ given by a bayesian posterior shows that this might not be trivial however.

A comparison of generalized hybrid Monte Carlo methods with and without momentum flip

February 8, 2016Importance Sampling, mcmc, Monte CarloIngmar

This experimental paper from 2009 by Akhmatskaya, Bou-Rabee and Reich in the Journal of Computational Physics takes a look at what in statistics people would call HMC with partial momentum refreshment.The paper got my attention mainly because I met Elena Akhmatskaya at MCMSki.

The ‘generalized’ in the paper refers to the fact that the momenta are not resampled at each new HMC step, but rather according towhere $p_i \sim \mathcal{N}(0,\Sigma)$ is the old momentum, and we mix it with another Gaussian RV of the same distribution $u_i$ for some parameter $\phi$ . We recover HMC for $\phi=\pi/2$ , as in that case the momentum is always refreshed.

Also, they are looking at a so-called shadow HMC variant, which really samples from a Hamiltonian system that is not the original one, but close to it. Correction for sampling from the wrong distribution is done by importance weighting (when she was telling me that I thought “I knew IS could work in high dimensions!”, as they sample from up to 10,000 dimensions and do better than HMC!).

Now the main gist of the paper is that they where trying to get rid of momentum flips in the case of rejection of the proposal, as it was previously thought that momentum flips lead to a worse sampler. The intuition would be that a momentum flip leads you back to where you started. However, the finding is that to the contrary, their version without flip (that still satisfies a detailed balance criterion) does worse in actual estimation tasks than the conservative Generalized Shadow HMC (GSHMC) sampler. I like when things stay easy. But as this paper does not describe the actual GSHMC method in detail, I will have to go back to the original paper, as my interest is sparked.

Streaming weighted updates of cholesky factors

January 27, 2016Importance Sampling, Monte Carlo, Numerics, SMCIngmar

… are hell. Heiko and I have been spending the day trying to get code to work for a numerically stable streaming update of a Cholesky factor in an adaptive Importance Sampling setting. This is less then trivial, also because it has to be done in a weighted fashion (because of Importance Sampling) and weights should be kept in logspace for stability. Thinking I will have to go through this again for an Eigendecompositon instad of Cholesky for a collaboration planned with Mathieu Gerber does not make things easier to stomach.
This day again strengthens my wish to move more in the direction of Judith-Russeau-statistics, i.e. away from computers, towards pen and paper.

PS: Does anybody have code solving exactly this problem (we have tons for almost this problem)?

A Repulsive-Attractive Metropolis Algorithm for Multimodality

January 26, 2016Inference, mcmc, Monte CarloIngmar

(Title image from Wikipedia)

Christian put my nose on this preprint by Tak, Meng and van Dyk a few days ago, so during the flight from Berlin to Paris today I sniffed on it. It was a very interesting read and good to get my thoughts away from the fact that I was an Opfer of German friendliness at airport security.
The basic idea is to design a random walk MH algorithm for targets with multiple and distant modes. The distant is important here, because for very close modes simple Adaptive Metropolis (Haario et al. 2001), which is simply using a scaled version of the targets covariance in a Gaussian random walk, should work pretty well.

Which it probably does not for the targets above, as such a proposal would often end up in areas of low posterior density.
Now the idea is the following: given current state $x_i$ of the Markov Chain, the final MH proposal $x''$ is constructed using an intermediate step $x'$ , where the intermediate step is encouraged to have lower density than $x_i$ under the target, while $x''$ is encouraged to have higher density than the intermediate step. Hoping that the intermediate step gets you out of a mode and the consecutive step into a new mode. This is achieved by using the inverse MH-ratio for encouraging moves to a valley in the target, while the standard MH-ratio is used for moving uphill again. Of course computing the final acceptance probability $\alpha(x''|x_i)$ involves computing an intractable integral, as one has to integrate away the intermediate downhill move. They get around this by introducing an auxiliary variable, a technique inspired by Møller et al. (2006), where it was used to get around the computation of normalizing constants. I discussed a similar idea shortly with Jeff Miller (currently at Duke) one and a half years ago when we worked on the estimation of normalizing constants though using gradient information.
Am main argument for their algorithm is that it only needs tuning of a single scale parameter, whereas other MCMC techniques for multimodal targets are notoriously hard to tune.
In evaluation they compare to tempered transitions and equi-energy samplers and perform better both with respect to computing time and MSE. And of course human time invested in tuning.
However, I’m slightly tempted to repeat Nicolas mantra here “just use SMC”. Or slightly change the mantra to “… PMC” – because this is easier to stomach for MCMC-biased researchers, or so I believe. Of course this adds the number of particles to tuning, but that might be tuned automatically using the recent paper of the Spanish IS-connection.

Layered adaptive Importance Sampling

January 25, 2016Inference, mcmc, SMCIngmar

This arXival from last spring/summer by Martino, Elvira, Luengo and Corander combines and extends upon recent advances of Importance Sampling, using mainly ideas from Adaptive Multiple lmportance Sampling (AMIS) and Population Monte Carlo (PMC). The extension consists of the idea to not use the Importance Sampling procedure itself to come up with new proposal distributions, but rather to run a Markov Chain. The output of which is used solely as the location parameter for IS proposal distributions $q_{n,t}$ . The weights of the samples drawn from these are Rao-Blackwellized using the deterministic mixture idea of Zhou and Owen, and as far as I can see only the Importance Samples are used for estimating integrands.
What’s most striking for me as somebody who has thought about these methods a lot during the PhD is the idea that in principle one is free to Rao-Blackwellize using an arbitrary partition of the samples/proposal distributions and still get a consistent estimator. Xi’an mentioned this to me earlier and of course it is not surprising given that even without Rao-Blackwell my Gradient IS did considerably better than some Adaptive MCMC algorithms. However this paper makes that idea transparent and uses it extensively. The main idea that is put forward however is to use (parallel) MCMC with the same target for coming up with IS-proposal locations. The output of MCMC is only used for that purpose but not for estimation. Which seems kind of wasteful, but in a nice conversation over email the first author Luca Martino assured me that recycling proposals as both IS and MH proposals made performance go down because of correlations. I don’t get an intuition for why that would be the case, but maybe I’ll have to fall on my own nose for that. What I like about this particular idea of getting locations from MCMC is that one is free from the tuning problem I’ve hit upon in GRIS: if you scale up the proposal covariance in GRIS (or in the PMC approach from the Cappé 2004 paper), you can get an arbitrarily high ESJD – together with a really bad target approximation. Thus unmodified ESJD cannot be used for tuning. And neither can acceptance rate which doesn’t exist. Using MCMC for getting proposal locations is an elegant way around that problem. The effect of this is shown in the plot from the paper below, where the two rightmost plots show one of their methods.

Some other aspects about the paper I find less clear. For instance, I’m not sure about the abundance of different algorithms that are introduced. It leaves the impression that the authors where trying to do mass instead of class (something I might make myself guilty of these weeks as well). Also, while the targets they use for evaluation are fine, only reporting the MSE of one dimension of one integrand seems odd. One simple thing here might be to report the MSE averaged over dimensions as well, another to report the MSE of an estimate of the target distributions variance/higher order moments.

(Title image (c) Carlos Delgado, CC-BY-SA)

Why the MAP is a bad starting point in high dimensions

January 21, 2016Inference, mcmc, Monte Carlo, SMC, statsIngmar

During MCMSki 2016, Heiko mentioned that in high dimensions, the MAP is not a particularly good starting point for a Monte Carlo sampler, because there is no volume around it. I and several people smarter than me where not sure why that could be the case, so Heiko gave us a proof by simulation: he sampled from multivariate standard normals with increasing dimensions and plotted the euclidean norm of the samples. The following is what I reproduced for sampling a standard normal in $D=30$ dimensions.The histogram has a peak at about $\sqrt{D}$ , which means most of the samples are in a sphere around the mean/mode/MAP of the target distribution and none are at the MAP, which would correspond to norm $0$ .

We where dumbstruck by this, but nobody (not even Heiko) had an explanation for what was happening. Yesterday I asked Nicolas about this and he gave the most intuitive interpretation: Given a standard normal variable in $D$ dimensions, $x \sim \mathcal{N}(0,I_D)$ , computing the euclidean norm you get $n^2 = \|x\|^2 = \sum_{i=1}^D x_i^2$ . But as $x$ is gaussian, this just means $n^2$ has a $\chi^2(D)$ distribution, which results in the expected value $\mathbb{E}(n) = \sqrt{D}$ . Voici l’explication.

(Title image (c) Niki Odolphie)

Kernel Adaptive Sequential Monte Carlo

December 18, 2015Inference, Monte Carlo, SMC, tall big dataIngmar

Heiko Stratmann, Dino Sejdinovic, Brooks Paige and myself had a poster on our work on Kernel Adaptive SMC (arXiv) at the Scalable Inference NIPS workshop this year. The basic idea is very related to Dinos paper on Kernel-informed MCMC, in that the particle system is (implicitly) mapped to a function space (the infamous Reproducing Kernel Hilbert Space) and used to inform a sample from a Gaussian fit to the functional associated with samples. As always, things that are nasty and nonlinear in the input space behave much more nicely in feature space. An when your name is Dino Sejdinovic, you can actually integrate out all steps in feature space, ending up with a Gaussian proposal in the space you actually want to sample from.

In the title cartoon, our approach (in red, called KASS for Kernel Adaptive SMC sampler) lines up nicely with the support of the target distribution. ASMC by Fearnhead et al., or at least the sampler they use in their evaluation, which is a special case of our method, cannot adapt to this nonlinear structure. This results in better performance for KASS compared to ASMC and Random Walk SMC, as measured by Maximum Mean Discrepancy.However, this of course comes at the price of higher computational complexity, similar to related methods such as Riemannian Manifold MALA/HMC. If your dataset is large however and evaluating the likelihood majorizes evaluating the Gram matrix on your particle system, this method will still have an edge over others when the support is nonlinear. For the MCMC predecessor KAMH/Kameleon see Heikos post.

Optimization Monte Carlo

December 15, 2015Monte Carlo, UncategorizedIngmar

A very short note on Optimization Monte Carlo by Meeds and Welling. Max Welling gave a talk on this at a NIPS workshop, during which unfortunately I wasn’t very attentive. Unfortunately because they propose essentially the same thing as David Duvenaud and coauthors did in Early stopping is nonparametric variational inference, which I was super-vocal in criticizing just 2h earlier at Davids poster. Now because I didn’t closely listen at Max’ talk and because it was Max Welling rather than David, I wasn’t all so vocal, but took the discussion with Max offline.

(The following critique is not actually valid for this paper, read the edit)

The critique is essentially the same: if you draw an RV and then optimize it, you can’t compute the Jacobian to correct for the transformation, because the transformation is typically not bijective (think gradient ascent: let $y = \lambda \nabla \log f(x)$ . Now what is the inverse step when you only know $y$ but not $x$ and thus can’t know $\nabla \log f(x)$ ? It doesn’t exist in general). Which makes the very basis of the method unsound. Max answered that one can still compute the Jacobian in certain cases, even if the inverse function doesn’t exist. For some reason I wasn’t able to counter that on the spot. Of course, you can always compute the Jacobian of the forward transformation, but you don’t need that Jacobian. The Jacobian that you need is that of the inverse function. See Theorem 12.7 in Jacod & Protter for example.

I’ll stop here, as I asked Xi’an for his opinion and he will post about this as well, presumably with a more detailed discussion. If Ted Meeds and Max Welling answer to my email on this and prove me wrong, I’ll update this post of course.

EDIT 1: Lesson learned. I shouldn’t post with only half understanding the paper (if half is not said too much). They don’t actually suggest optimizing an RV and computing the Jacobian of the transformation. Rather, they propose optimizing another variable, which is not taken to be random (the parameters of a simulator, which is specific to the ABC setting).

EDIT 2: Xi’ans post

Character-Aware Neural Language Models

December 14, 2015language models, Models, Neural Networks, statsIngmar

I’m taking a friends questions on Vector Space Semantics models as a reason to write about this arXival by Kim, Jernite, Sontag and Rush using an idea I’ve had in the back of my mind while fighting my semantics model: that maybe it is easier to model characters directly instead of words, as there are only so many characters but hundreds of thousands of words. And modeling characters directly might give an algorithm robustness to neologisms and spelling mistakes. Which indeed seems to be one of the conclusions of the paper.

The basic idea is to use character level ConvNets (with a pooling operation over time), extract features using the recently proposed autobahn networks (see my post) and bind things together over time using LSTMs. The big thing is that one has far fewer parameters than when processing at the word level, while the downside is that I’m not completely sure how easily one might extract word embeddings. While that might be no problem in the long run (as I suppose models could be developed that work based on characters only), it might be a problem for quick combination of this papers approach with current mainstream tools used in the industry.

In the convolutional layer, they used between 100 and 1000 filters of varying length, each of which basically recognizes different n-grams. After max pooling (over time), ~~autobahn~~ highway layers give a way of extracting hierarchical features. LSTMs are then used to predict the next word, the loss/”likelihood” being cross entropy to the actually observed next word. Unsurprisingly, in their discussion they account a strong increase in performance to the highway layers. Making me again think that we have to work on enabling deeper hierarchies for Bayesian Models.

Overall a super interesting case study, though as a linguist I would really like to know how these models could be changed to give us some insight into the structure of the language. As a plus for my friend, the code is available on github, written using the ubiquitius Torch library.