This arXival from last spring/summer by Martino, Elvira, Luengo and Corander combines and extends upon recent advances of Importance Sampling, using mainly ideas from Adaptive Multiple lmportance Sampling (AMIS) and Population Monte Carlo (PMC). The extension consists of the idea to not use the Importance Sampling procedure itself to come up with new proposal distributions, but rather to run a Markov Chain. The output of which is used solely as the location parameter for IS proposal distributions . The weights of the samples drawn from these are Rao-Blackwellized using the deterministic mixture idea of Zhou and Owen, and as far as I can see only the Importance Samples are used for estimating integrands.
What’s most striking for me as somebody who has thought about these methods a lot during the PhD is the idea that in principle one is free to Rao-Blackwellize using an arbitrary partition of the samples/proposal distributions and still get a consistent estimator. Xi’an mentioned this to me earlier and of course it is not surprising given that even without Rao-Blackwell my Gradient IS did considerably better than some Adaptive MCMC algorithms. However this paper makes that idea transparent and uses it extensively. The main idea that is put forward however is to use (parallel) MCMC with the same target for coming up with IS-proposal locations. The output of MCMC is only used for that purpose but not for estimation. Which seems kind of wasteful, but in a nice conversation over email the first author Luca Martino assured me that recycling proposals as both IS and MH proposals made performance go down because of correlations. I don’t get an intuition for why that would be the case, but maybe I’ll have to fall on my own nose for that. What I like about this particular idea of getting locations from MCMC is that one is free from the tuning problem I’ve hit upon in GRIS: if you scale up the proposal covariance in GRIS (or in the PMC approach from the Cappé 2004 paper), you can get an arbitrarily high ESJD – together with a really bad target approximation. Thus unmodified ESJD cannot be used for tuning. And neither can acceptance rate which doesn’t exist. Using MCMC for getting proposal locations is an elegant way around that problem. The effect of this is shown in the plot from the paper below, where the two rightmost plots show one of their methods.

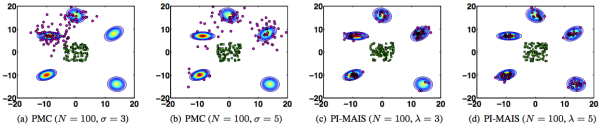
Some other aspects about the paper I find less clear. For instance, I’m not sure about the abundance of different algorithms that are introduced. It leaves the impression that the authors where trying to do mass instead of class (something I might make myself guilty of these weeks as well). Also, while the targets they use for evaluation are fine, only reporting the MSE of one dimension of one integrand seems odd. One simple thing here might be to report the MSE averaged over dimensions as well, another to report the MSE of an estimate of the target distributions variance/higher order moments.

(Title image (c) Carlos Delgado, CC-BY-SA)